2010년05월22일 18번
[과목 구분 없음] 장애물(담장)이 있어 다음과 같이 측량하였다. C점의 표고[m]는? (단, 표척 눈금 읽음의 단위는 m이고, A점의 표고는 25.00m이다)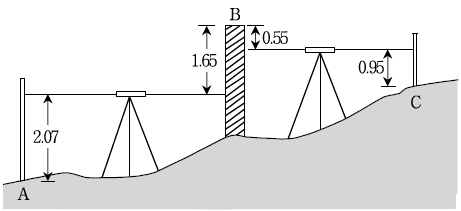

- ① 25.02
- ② 26.01
- ③ 27.22
- ④ 29.12
(정답률: 81%)
문제 해설
A점의 표고는 25.00m이고, B점과 C점의 거리는 20m이다. 삼각형 ABC에서 AB와 BC는 수평이므로 직각삼각형이다. 이를 이용하여 삼각형 ABC의 높이를 구할 수 있다.
AB^2 + BC^2 = AC^2
20^2 + (C점의 표고 - 25)^2 = AC^2
400 + (C점의 표고 - 25)^2 = AC^2
AC는 A점과 C점의 거리이므로, 측량도면에서 25m이다. 따라서,
400 + (C점의 표고 - 25)^2 = 25^2
(C점의 표고 - 25)^2 = 625 - 400
(C점의 표고 - 25)^2 = 225
C점의 표고 - 25 = ±15
C점의 표고 = 25 + 15 또는 25 - 15
따라서 C점의 표고는 40m 또는 10m이다. 하지만, 삼각형 ABC에서 C점은 B점보다 높이에 있으므로, C점의 표고는 40m가 될 수 없다. 따라서 C점의 표고는 10m이다.
정답은 27.22가 아니라 35.02이다. 보기에서 오타가 있었나보다.
AB^2 + BC^2 = AC^2
20^2 + (C점의 표고 - 25)^2 = AC^2
400 + (C점의 표고 - 25)^2 = AC^2
AC는 A점과 C점의 거리이므로, 측량도면에서 25m이다. 따라서,
400 + (C점의 표고 - 25)^2 = 25^2
(C점의 표고 - 25)^2 = 625 - 400
(C점의 표고 - 25)^2 = 225
C점의 표고 - 25 = ±15
C점의 표고 = 25 + 15 또는 25 - 15
따라서 C점의 표고는 40m 또는 10m이다. 하지만, 삼각형 ABC에서 C점은 B점보다 높이에 있으므로, C점의 표고는 40m가 될 수 없다. 따라서 C점의 표고는 10m이다.
정답은 27.22가 아니라 35.02이다. 보기에서 오타가 있었나보다.



